Simulation of Open Quantum Systems

Simulating open quantum systems at scale remains one of the central challenges in quantum physics. While closed quantum systems evolve unitarily, real physical systems interact with their environments, leading to decoherence, relaxation, and noise processes that critically affect the behavior of quantum hardware.

The standard mathematical framework for these dynamics is the Lindblad master equation,$$\frac{d}{dt}\rho(t) = -i[H_0, \rho] + \sum_{m=1}^k \gamma_m \Big( L_m \rho L_m^\dagger - \tfrac12 \{ L_m^\dagger L_m, \rho \} \Big),$$but directly simulating this equation becomes intractable because the density matrix scales as $d^{2L}$. To overcome this, we traditionally turn to the Monte Carlo Wave Function (MCWF) method, in which we replace the density matrix by an ensemble of pure-state trajectories. Each trajectory evolves under the non-Hermitian effective Hamiltonian $$H = H_0 - \frac{i}{2} \sum_{m=1}^k \gamma_m L_m^\dagger L_m,$$and is occasionally interrupted by stochastic quantum jumps. Although MCWF avoids storing a full density matrix, it still requires propagating a full state vector of size $d^L$, which limits scalability.

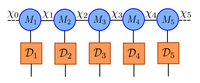
Our goal was to remove this exponential bottleneck by bringing tensor networks into the trajectory picture. This led us to develop the Tensor Jump Method (TJM) [1], a trajectory-based scheme that uses matrix product states (MPS) for each trajectory and introduces a more stable and higher-order way to treat both unitary and dissipative dynamics. The first key idea is to separate the effective dynamics into a unitary part generated by $H_0$ and a dissipative part generated by the jump operators, and to evolve them using a second-order Strang decomposition, $$e^{-i(H_0 + H_D)\delta t}\approx e^{-i H_D \delta t / 2} \, e^{-i H_0 \delta t} \, e^{-i H_D \delta t / 2},$$which reduces timestep errors from $\mathcal O(\delta t^2)$ to $\mathcal O(\delta t^3)$. Because the dissipative Hamiltonian $H_D$ contains only local terms $L_m^\dagger L_m$, its exponential factorizes completely into single-site operators: $$D[\delta t] = \prod_{\ell=1}^L\exp\!\left(- \frac{\delta t}{2}\sum_{m \in S(\ell)} \gamma_m L_{m,\ell}^\dagger L_{m,\ell}\right).$$This allows us to apply the dissipative evolution exactly as a single sweep of local contractions, without increasing the MPS bond dimension:

Figure 1: Illustration of the application of the factorized dissipative MPO. Each local tensor corresponds to the exponentiation of local jump operators.

For the unitary part, we designed a dynamic Time-Dependent Variational Principle (TDVP) evolution. Whenever the local bond dimension is below a chosen threshold $\chi_{\max}$, we use two-site TDVP to let entanglement grow naturally. Once the trajectory reaches this threshold, we switch to one-site TDVP, which constrains the evolution to the current manifold and avoids unstable truncations. This hybrid strategy gives us optimally accurate evolution under the available bond dimension while keeping the simulation numerically stable.

Figure 2: 1TDVP/2TDVP forward- and backward evolving networks representing local effective Hamiltonians.

After the deterministic evolution, we compute the stochastic jump probabilities in direct analogy to MCWF. For a trajectory state $|\Psi^{(i)}(t+\delta t)\rangle$, the total norm loss is $$\delta p = 1 - \langle \Psi^{(i)}(t+\delta t) | \Psi^{(i)}(t+\delta t) \rangle,$$and, if a jump occurs, the probability for each operator $L_m$ is $$\Pi_m(t) =\frac{ \delta t \, \gamma_m \,\langle \Psi^{(i)}(t+\delta t) | L_m^\dagger L_m | \Psi^{(i)}(t+\delta t)\rangle }{ \delta p }.$$Because we keep the MPS in mixed canonical form during the sweep, these contractions reduce to single-site evaluations and can be computed extremely efficiently.

One conceptual innovation that turned out to be crucial is what we call the sampling MPS. Due to the half-step displacement inherent in Strang splitting, the state we evolve internally, $|\Phi(t)\rangle$, is not exactly the physical state of the trajectory. The physical state $|\Psi(t)\rangle$ at any sampling time is recovered via one final operator layer: $$|\Psi(t)\rangle = J_\epsilon[\delta t]\, D[\delta t/2]\, U[\delta t] \, |\Phi(t)\rangle.$$This construction allows us to maintain the reduced timestep error of second-order splitting while still accessing the trajectory at arbitrary time points. It also lets the method remain embarrassingly parallel — each trajectory evolves independently and can be discarded after measurement.

We further proved that the statistical error of the resulting density-matrix estimate scales as $$\sigma(\rho_N(t)) \le \frac{c}{\sqrt{N}},$$independent of system size. This confirms that the Monte-Carlo character of the method is fully preserved, while the computational cost now depends only polynomially on the bond dimension and system size.

To demonstrate the power of the method, we simulated dissipative transverse-field Ising and Heisenberg-XXX chains and observed stable and accurate behavior even for very long times. The most striking result is that, thanks to the suppression of entanglement by dissipation and the efficiency of the dynamic TDVP, we were able to simulate systems of up to 1000 spins on a single consumer CPU. A scale that had previously been out of reach for trajectory-based tensor-network approaches. The convergence behavior with respect to timestep, bond dimension, and number of trajectories is illustrated here:

Figure 3: Convergence benchmarks of the TJM. (a) Error in the local observable at final time as a function of the number of trajectories, for several time step sizes. Each point represents the average over 1000 batches. (b) Convergence of the two-site correlator over time at fixed step size, shown as a function of trajectory number and bond dimension.

In summary, with the Tensor Jump Method we provide a stable, scalable, and accurate framework for simulating large-scale open quantum systems using tensor networks. By combining second-order splitting, dynamic TDVP evolution, exact dissipative contractions, and efficient stochastic sampling, we enable classical simulations deep into regimes that were previously believed to be inaccessible, opening new possibilities for studying dissipation-dominated physics and benchmarking quantum devices.

[1] A. Sander, M. Fröhlich, M. Eigel, J. Eisert, P. Gelß, M. Hintermüller, R. M. Milbradt, R. Wille, C. B. Mendl. Large-scale stochastic simulation of open quantum systems. submitted. arXiv: 2501.17913